E1 利用傅里叶变换红外光谱法Fourier transform infrared spectroscopy测定甲酸的二聚热heat of dimerization

Giles Henderson

东伊利诺伊大学，查尔斯顿，伊利诺伊州 61920

尽管微型计算机在大学中日益普及，但典型的大学物理化学physical chemistry实验教材并未描述能充分利用其能力的实验。本文将描述如何根据二聚体dimer平衡常数equilibrium constant的温度依赖性temperature dependence来测定甲酸的二聚热heat of dimerization。实验中采用计算机对红外干涉图interferogram进行傅里叶变换Fourier transform得到透射光谱transmission spectrum，将透射率transmittance转换为吸光度absorbance，进行光谱扩展，通过光谱乘法和光谱减法spectral subtraction分离单体monomer和二聚体dimer的贡献，并通过光谱积分spectral integration确定蒸气组分vapor components，此外还进行最小二乘拟合least-squares fitting和数字绘图digital plotting。尽管该项目是使用配备商业软件的 Nicolet 20DXB 型傅里叶变换红外光谱仪Fourier transform infrared spectrometer完成的，但只要与微型计算机连接，该测量也可以轻松地用传统色散型仪器dispersive instrument进行（1）。

甲酸二聚体dimer形成的热力学thermodynamics

羧酸分子即使在气相中也存在强烈的缔合作用association。早期的电子衍射electron diffraction研究（2）表明，甲酸蒸气中富含一种由两个氢键hydrogen bond稳定的平面二聚体dimer形式（见图1）。单体monomer-二聚体dimer平衡equilibrium，

2CH2O2⇄(CH2O2)2+ 热 \begin{equation*} 2 \mathrm{CH}_{2} \mathrm{O}_{2} \rightleftarrows\left(\mathrm{CH}_{2} \mathrm{O}_{2}\right)_{2}+\text { 热 } \tag{1} \end{equation*}

可用平衡常数equilibrium constant表示

KD=P(CH2O2)2/P2(CH2O2)\begin{equation*} K_{\mathrm{D}}=P\left(\mathrm{CH}_{2} \mathrm{O}_{2}\right)_{2} / P^{2}\left(\mathrm{CH}_{2} \mathrm{O}_{2}\right) \tag{2} \end{equation*}

其中组分 i 的活度activity由其分压partial pressure PiP_{\mathrm{i}} 给出。预计蒸气的红外光谱infrared spectrum将表现为单体monomer和二聚体dimer特征峰characteristic peaks重叠的混合谱。

从方程 2 可以明显看出，二聚体dimer的浓度将随单体monomer分压partial pressure的平方而增加。因此，样品压力的变化预计会引起单体monomer与二聚体dimer比例的变化。这提示了通过适当的数据处理来分离重叠的单体monomer和二聚体dimer光谱的可能性。 由于二聚体dimer的形成是放热过程exothermic process，因此平衡equilibrium（方程1）预计会向左移动，即在高温下有利于高浓度的单体monomer和低浓度的二聚体dimer。如果单体monomer和二聚体dimer的特征峰characteristic peaks能够完全分辨，并且已知相应的比尔定律Beer's law积分吸收系数integrated absorption coefficient，那么平衡equilibrium混合物的组成和平衡常数equilibrium constant的值就可以通过红外吸收光谱infrared absorption spectroscopy实验确定。假设蒸气组分vapor components为理想气体ideal gas，则 Pi=[i]RTP_{\mathrm{i}}=[\mathrm{i}] R T。

图 1. 甲酸二聚体dimer的 C2hC_{2 h} 结构。

图 2. 甲酸蒸气在 20∘C20^{\circ} \mathrm{C} 和约 0.01 atm 下的傅里叶变换红外吸收光谱Fourier transform infrared absorption spectrum。该光谱使用 10 cm KBr 吸收池，扫描 20 次，分辨率resolution为 4−cm−14-\mathrm{cm}^{-1}。

KD=[(CH2O2)2][CH2O2]2RT=⟨D⟩⟨M⟩2T(⟨ϵM⟩2l⟨ϵD⟩R)\begin{equation*} K_{\mathrm{D}}=\frac{\left[\left(\mathrm{CH}_{2} \mathrm{O}_{2}\right)_{2}\right]}{\left[\mathrm{CH}_{2} \mathrm{O}_{2}\right]^{2} R T}=\frac{\langle\mathrm{D}\rangle}{\langle\mathrm{M}\rangle^{2} T}\left(\frac{\left\langle\epsilon_{\mathrm{M}}\right\rangle^{2} l}{\left\langle\epsilon_{\mathrm{D}}\right\rangle R}\right) \tag{3} \end{equation*}

其中 [i] 是组分 i 的摩尔浓度molar concentration，⟨D⟩\langle\mathrm{D}\rangle 是二聚体dimer一个完全分辨的红外谱带band的积分吸收integrated absorbance。⟨M⟩\langle\mathrm{M}\rangle 是一个分辨的单体monomer谱带band的积分吸收integrated absorbance，⟨ϵD⟩\left\langle\epsilon_{\mathrm{D}}\right\rangle 和 ⟨ϵM⟩\left\langle\epsilon_{\mathrm{M}}\right\rangle 分别是二聚体dimer和单体monomer相应的积分吸收系数integrated absorption coefficient，ll 是光程path length，而 RR 是气体常数gas constant。此外，KDK_{\mathrm{D}} 将根据 ΔHD\Delta H_{\mathrm{D}} 的大小随温度temperature变化：

ΔGD∘=−RTln⁡(KD)=ΔHD∘−TΔSD∘\begin{equation*} \Delta G_{\mathrm{D}}^{\circ}=-R T \ln \left(K_{\mathrm{D}}\right)=\Delta H_{\mathrm{D}}^{\circ}-T \Delta S_{\mathrm{D}}^{\circ} \tag{4} \end{equation*}

其中 ΔGD∘,ΔHD∘\Delta G_{\mathrm{D}}^{\circ}, \Delta H_{\mathrm{D}}^{\circ} 和 ΔSD∘\Delta S_{\mathrm{D}}^{\circ} 分别是二聚反应dimerization reaction的标准自由能free energy、焓enthalpy和熵entropy。如果我们将方程 3 代入 KDK_{\mathrm{D}} 并重新整理，可以很容易地得到

ln⁡(⟨D⟩⟨M⟩2T)=−ΔHD∘R(1T)+[ΔSD∘R−ln⁡(⟨ϵM⟩2l⟨ϵD⟩R)]\begin{equation*} \ln \left(\frac{\langle\mathrm{D}\rangle}{\langle\mathrm{M}\rangle^{2} T}\right)=\frac{-\Delta H_{\mathrm{D}}^{\circ}}{R}\left(\frac{1}{T}\right)+\left[\frac{\Delta S_{\mathrm{D}}^{\circ}}{R}-\ln \left(\frac{\left\langle\epsilon_{\mathrm{M}}\right\rangle^{2} l}{\left\langle\epsilon_{\mathrm{D}}\right\rangle R}\right)\right] \tag{5} \end{equation*}

因此，只需要知道吸收光谱absorption spectrum的温度依赖性temperature dependence，就可以确定 ΔHD∘\Delta H_{\mathrm{D}}^{\circ} 以及二聚体dimer中的氢键能hydrogen bond energy。

1 实验部分

将几滴试剂级甲酸（Fisher A-118）放入一个配有水银压力计manometer和液氮冷阱cold trap的真空管路vacuum line贮存器中。使用一根两端配有球形接头的 1 米长派热克斯玻璃管将真空管路vacuum line连接到一个 10 cm 长的 KBr 气体池gas cell。气体池gas cell用加热带包裹，并配备一个热敏电阻thermistor探头，以将池温维持在 0.1∘C0.1^{\circ} \mathrm{C} 的精度。将气体池gas cell安装在 Nicolet 20DXB 型傅里叶变换红外光谱仪Fourier transform infrared spectrometer中。由于需要吹扫单光束干涉仪single-beam interferometer以排除 CO2\mathrm{CO}_{2} 和 H2O\mathrm{H}_{2} \mathrm{O} 蒸气，因此在整个实验期间，样品池保持不动，其派热克斯连接管和电线被密封在已吹扫的样品仓内。将大约 0.01 atm 的甲酸蒸气转移到气体池gas cell中，并加入 N2\mathrm{N}_{2} 使总压达到 1 atm。图 2 展示了由 20 个干涉图interferogram经傅里叶变换Fourier transform得到的典型

图 3. 甲酸蒸气光谱的选定部分。上方的谱线是在 0.010 atm 下扫描 20 次得到的，下方的谱线是在 0.0025 atm 下扫描 320 次得到的。图中给出了两个特征峰characteristic peaks的积分吸收integrated absorbance比，这使得可以对单体monomer和二聚体dimer的谱带band进行归属。

图 4. 此处通过高压和低压蒸气光谱的适当线性组合，分别以“正残差光谱residual spectrum”和“负残差光谱residual spectrum”的形式获得了二聚体dimer和单体monomer的吸收光谱absorption spectra。

4−cm−14-\mathrm{cm}^{-1} 分辨率resolution光谱。然后将样品稀释至约原浓度的 1/4，并采集 320 次扫描的光谱。扫描次数增加了 (4)2{^2} 倍，以保持与较浓样品相同的信噪比signal-to-noise ratio。在室温至 45.0∘C45.0^{\circ} \mathrm{C} 范围内的五个不同温度下重复此过程，并将数字化光谱存储在软盘上以备后续数据处理。

2 数据处理

图 3 比较了两种不同压力下甲酸蒸气光谱选定部分的放大图。我们注意到，由于甲酸压力的增加，位于 1105 cm−11105 \mathrm{~cm}^{-1} 的特征峰characteristic peak的积分吸收integrated absorbance增加了 1.66 倍，而位于 1218 cm−11218 \mathrm{~cm}^{-1} 的特征峰characteristic peak的积分吸收integrated absorbance增加了 2.80≃(1.66)22.80 \simeq (1.66)^{2} 倍。1218−cm−11218-\mathrm{cm}^{-1} 谱带band的二次方压力依赖性pressure dependence使我们能将其归属于二聚体dimer，而将 1105−cm−11105-\mathrm{cm}^{-1} 的信号归属于单体monomer。现在，如果我们将整个低压光谱乘以 1.66，然后从高压光谱中减去它，我们预计所有单体monomer的特征峰characteristic peaks都将被完全抵消，得到的正残差吸收positive residual absorbance将归因于二聚体dimer。同样地，如果我们将整个低压光谱乘以 2.80，然后从高压光谱中减去它，所有二聚体dimer的贡献都将被完全抵消。

甲酸吸收蒸气组分vapor components

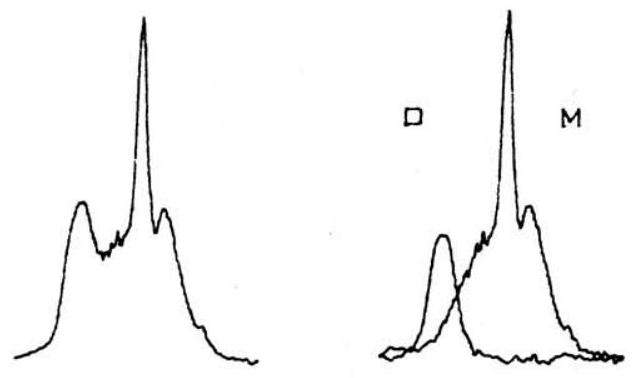
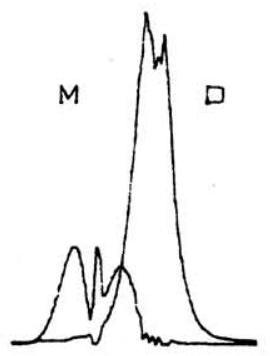
图 5. 这里描述的技术为分离重叠的吸收带absorption bands提供了一种强大的数值方法。上方谱线给出了 760 至 530 cm−1530 \mathrm{~cm}^{-1} 之间吸收的单体monomer和二聚体dimer组分，下方谱线给出了 1830 至 1680 cm−11680 \mathrm{~cm}^{-1} 之间 C=O 伸缩振动模式stretching vibration mode的组分。

图 6. 红外吸收的温度依赖性temperature dependence。单体monomer的 C-O 伸缩振动带stretching vibration band（位于 1105 cm−11105 \mathrm{~cm}^{-1}）随温度升高而增强，而二聚体dimer的 C-O 伸缩振动带stretching vibration band（位于 1218 cm−11218 \mathrm{~cm}^{-1}）则相应减弱。

然而，在这种情况下，我们将过度减去单体monomer的贡献，因此会得到一个单体monomer的“负残差光谱residual spectrum”。这两种结果都显示在图 4 中。我们注意到，如图 5 所示，单体monomer和二聚体dimer的特征峰characteristic peaks得到了非常令人满意的分离，尤其是在谱带band重叠的区域。当我们注意到图 2 中单体monomer的 2945−cm−12945-\mathrm{cm}^{-1} C-H 伸缩振动模式stretching vibration mode如何被重叠的二聚体dimer吸收完全掩盖，而在图 4 中这个弱谱带band又如何清晰地显现出来时，我们就能进一步体会到该技术的价值。

表 1. 甲酸吸收的温度依赖性temperature dependence a { }^{\text {a }}

t(∘C)t\left({ }^{\circ} \mathrm{C}\right) Pb\mathrm{P}^{b} ⟨ D ⟩1218\langle\text { D }\rangle_{1218} ⟨M⟩1105\langle\mathrm{M}\rangle_{1105} ln⁡(⟨D⟩/⟨M⟩2T)\ln \left(\langle\mathrm{D}\rangle /\langle\mathrm{M}\rangle^{2} T\right)
29.1 h 22.4222.4_{2} 16.5116.5_{1} -8.21
29.1 l 8.0128.01_{2} 9.9549.95_{4} -8.23
33.0 h 30.5430.5_{4} 21.7221.7_{2} -8.46
33.0 l 9.9049.90_{4} 12.3812.3_{8} -8.46
37.0 h 30.6030.6_{0} 24.4524.4{ }_{5} -8.71
37.0 l 9.3789.37_{8} 13.5613.5_{6} -8.71
41.0 h 27.3827.3_{8} 25.7725.7_{7} -8.94
41.0 l 8.3018.30_{1} 14.3214.3_{2} -8.96
45.0 h 33.3533.3_{5} 31.5531.5_{5} -9.16
45.0 l 10.2710.2_{7} 17.6117.6_{1} -9.17

a⟨D⟩{a}\langle D\rangle 和 ⟨M⟩\langle M\rangle 分别对应于 1218 cm−11218 \mathrm{~cm}^{-1} 处的 ν6\nu_{6} 二聚体dimer谱带band（4）和 1105 cm−11105 \mathrm{~cm}^{-1} 处的 ν6\nu_{6} 单体monomer谱带band（3）的积分吸收integrated absorbance。 b h{b} \mathrm{~h} 和 l 分别代表约 0.010 和 0.0025 atm 的甲酸蒸气。

图 7. ΔH0\Delta H_{0} 从方程 5 对观测数据的最小二乘拟合least-squares fit的斜率中获得。此处 Q=⟨D⟩/⟨M⟩2TQ=\langle D\rangle /\langle M\rangle^{2} T。

有好奇心的学生可能希望将这些观测到的振动频率vibrational frequencies与最近对单体monomer（3）和二聚体dimer（4）进行简正坐标分析normal coordinate analysis所计算出的值进行比较。

既然我们有了一种能精确分离单体monomer和二聚体dimer吸收的简单方法，我们就可以研究温度对平衡equilibrium组成的影响。图 6 显示了在五个温度下二聚体dimer（1218 cm−11218 \mathrm{~cm}^{-1}）和单体monomer（1105 cm−11105 \mathrm{~cm}^{-1}）的 C-O 伸缩振动带stretching vibration bands。我们注意到，单体monomer的吸收以二聚体dimer吸收的减少为代价而增加，这与放热反应exothermic reaction的预期相符。这些特征峰characteristic peaks的积分吸收integrated absorbance汇总于表 1。然后将这些结果用于方程 5 来获得二聚热heat of dimerization。ln⁡[⟨D⟩/(⟨M⟩2T)]\ln [\langle\mathrm{D}\rangle / \left.\left(\langle\mathrm{M}\rangle^{2} T\right)\right] 对 T−1T^{-1} 的作图见图 7。最小二乘least-squares斜率 (5.76±0.5)×103(5.76 \pm 0.5) \times 10^{3} 乘以 −R-R 得到 ΔHD∘=−47.9±0.4 kJ/mol\Delta H_{\mathrm{D}}^{\circ}= -47.9 \pm 0.4 \mathrm{~kJ} / \mathrm{mol}。该结果与表 2 中的其他文献值进行了比较。

3 讨论

从表 2 可以明显看出，关于甲酸的 ΔHD\Delta H_{\mathrm{D}} 值存在很大分歧。Coolidge (5) 进行的非常仔细的蒸气密度vapor density测量给出的实验结果高于吸收法absorption method测量的结果。这两种方法之间的差异或许是真实存在的，其原因在于蒸气密度vapor density法包含了所有类型的缔合association，而吸收法absorption method则不然。Herman (6) 报告的 ΔHD\Delta H_{\mathrm{D}} 值略高于本文测定的结果。

表 2. 甲酸的二聚热heat of dimerization

方法 年份 来源 ΔHb( kJ/mol)\Delta H_{b}(\mathrm{~kJ} / \mathrm{mol})
蒸气密度vapor density 1928 Coolidge (5) -59
红外吸收infrared absorption 1940 Herman (6) −52±3-52 \pm 3
LCAO-MO-SCF 1971 Clementi et al. (8) -67.8
最小基组basis set-STO-SCF优化结构optimized geometry 1976 Del Bene et al. (9) -63.2
双泽塔SCF（含畸变能） 1978 Smit et al. (10) -49.4
FTIR 本工作 −48.9±0.4-48.9 \pm 0.4

然而，这种差异可能是由于 Herman 使用了最大吸收波长wavelength λmax\lambda_{\text{max}} 处的吸收值，而非积分吸收integrated absorbance值。当温度变化时，相应转动能级rotational energy levels的玻尔兹曼布居Boltzmann population会发生变化，导致谱带形状band shape不同。这种现象可能导致在 λmax\lambda_{\text{max}} 处的表观吸收系数apparent absorption coefficient随温度变化而变化，从而在 ln⁡K\ln K 对 1/T1/T 的斜率中引入系统误差systematic error。通过对整个观测到的转动包络rotational envelope进行吸收积分，可以很明显地避免这个问题。Clague 和 Bernstein (7) 比较了这两种方法，同样观察到当使用谱带面积band area而非峰高peak height时，ΔHD\Delta H_{\mathrm{D}} 会降低 4−kJ/mol4-\mathrm{kJ} / \mathrm{mol}。

我们还注意到理论从头计算ab initio calculation值（8-10）之间也存在巨大差异。然而，随着基组basis set和优化几何构型optimized geometry的不断改进，这些计算结果正逐渐与实验光谱值experimental spectroscopic values趋于一致。

从方程 5 可以看出，如果已知积分吸收系数integrated absorption coefficient的精确值，就可以从图 7 的截距intercept中确定 ΔSDo\Delta S_{\mathrm{D}}^{\mathrm{o}}，精确到三位有效数字。这将需要精确的样品浓度，或者进行比简单水银压力计manometer所能达到的精度高一个数量级的压力测量。另一种方法是在足够高的温度下测量光谱，此时样品几乎 100% 解离dissociate，从而可以直接根据比尔定律Beer's law确定 ⟨ϵM⟩\left\langle\epsilon_{\mathrm{M}}\right\rangle。在此，我们根据最小二乘least-squares截距intercept（−27.3±0.2-27.3 \pm 0.2）和吸收系数absorption coefficient的合理限值，估计 ΔSD∘\Delta S_{\mathrm{D}}^{\circ} 为 −180±50 J/moldeg-180 \pm 50 \mathrm{~J} / \mathrm{mol} \mathrm{deg}。ΔS\Delta S 的符号证实了在二聚体dimer形成过程中熵entropy或无序度disorder的减少。

总而言之，这项傅里叶变换红外光谱Fourier transform infrared spectroscopy测量似乎非常适合现代大学物理化学physical chemistry实验室。它利用微型计算机的能力来完成那些否则会因计算量过大而无法进行的计算，并同时阐释了基本的热力学thermodynamics平衡equilibrium原理。该练习可以轻松地在两个 3 小时的实验课时内完成。或许，最高效的设备使用方式是在第一个课时收集一组数据，将所有光谱存储在软盘上，然后在第二个课时安排个别学生（或两人一组）进行键盘操作以完成数据处理。

4 参考文献

(1) Mattson, B. M.; Shepherd, T. R.; Solsky, J. F. J. Chem. Educ. 1985, 62, 690. (2) Karl, J.; Brockway, L. J. Amer. Chem. Soc. 1944, 66, 574. (3) Redington, R. J. Mol. Spectrosc. 1977, 65, 171. (4) Hagen, I.; Cyvin, S. J. Mol. Struct. 1971, 8, 159. (5) Coolidge, A. J. Amer. Chem. Soc. 1928, 50, 2166. (6) Herman, R. J. Chem. Phys. 1940, 8, 252. (7) Clague, A.; Bernstein, H. Spectrochim. Acta 1969, 25A, 593. (8) Clementi, E.; Mehl, J.; von Niessen, W. J. Chem. Phys. 1971, 54, 508. (9) Del Bene, J.; Kochenour, W. J. Amer. Chem. Soc. 1976, 98, 2041. (10) Smit, P.; Derissen, J.; van Duijneveldt, F. J. Chem. Phys. 1978, 69, 4241.